The applications in this group deal with calculations of the interactions of x-ray beams with optical elements or components. Typical cases are mirrors, multilayers and crystals.
All these applications require the calculation of the refraction index and attenuation coefficient of the materials in use. These calculations cannot be done quickly from first principles, therefore we have compiled a data base (DABAX, DAtaBAse for X-ray applications) with the "ingredients" of these parameters. One of the advantages of DABAX is the decoupling of the data from the calculations. We can easily change the files in the database without needing to change the programs. Furthermore, we included in most programs a menu that allows the user to chose the preferred data file.
The applications in this section are many cases redundant. The same kind of calculation (e.g., beam attenuation from materials) can be done using different programs, and the choice of one of them depends on the context of the calculations (in relation to other elements, etc.) or by user's preference.
This application is a font-end of the DABAX (DAtaBAse for X-ray applications) data files. It allows to inspect the data files, download new files to your local XOP installation, consult file documentation, view the numerical data and plot the data in the files. From this interface, it is possible to start applications that make some post-processing of the DABAX data to calculate different parameters of beamline components:
DABAX: xf1f2 (f1,f2 scat fact, refraction index, reflectivity)
DABAX: xCrossSec (Cross section/absorption)
DABAX: xFh (Crystal Structure Factors)
DABAX: xf0 (f0 scattering factor)
The scattering factors are used for building the refractive index of amorphous materials and the structure factor of crystalline materials.
The atomic scattering factor written as
![]()
where Q is the momentum transfer (Q=kf-ki, |k|=2p/l) and E is the photon energy. In the case of elastic scattering, Q2=(ki2-kf2)=ki2+kf2-2kikf=2Q2(1-cos2q) |Q|=2|k|sinq=4psinq/l, and 2q is the total angle of scattering of the photon (angle between ki and kf).
The first term, f0, is the non resonant scattering, and it is due to the scattering of the radiation by the electron cloud of the atom. It is proportional to the Thomson scattering (one electron). It is called atomic form factor or atomic scattering factor of the atom. The DABAX files f0_<name>.dat contain the elastic scattering factors (either a tabulation or a parametrisation) data . They can be visualized using the xf0 applocation.
The second f’ and third f" terms are the resonant term, also called anomalous scattering factor, even if there is nothing ”r;anomalous” with them. They are tabulated in the f1f2_<name>.dat DABAX data files.
From the f1f2 tabulated data, one may calculate many physical quantities in the xf1f2 application for amorphous material calculations.
The photoelectric cross section is directly related to f" by
![]()
and the mass absorption coefficient:
![]()
where NA/A is the number of atoms per gram. The linear absorption coefficient is:
![]()
The refraction index can be written as
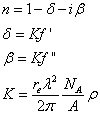
and from here it is possible to compute x-ray reflectivities for mirrors using the Fresnel formulas.
The information of the nature of compounds may be needed, which is stored in the file Compounds.dat.
For crystalline materials, information about the crystal cell and composition and structure is taken from the files CrystalStructures.dat and CrystalCell.dat. The the structure factor of a crystal is calculated by xfH using the relationship:
![]()
There are several possible type of interactions between an incident x-ray beam and a target material, and the cross-section for each will be different. These individual cross-sections are known as partial cross-sections. These are also called interaction channels. In the usual case that the interaction channels are independent (no interference effects between them), their overall sum is the total cross-section
![]()
Considering the interaction of x-rays and atoms, there are four main interaction channels:
Photoelectric absorption: the incident photon is absorbed by an atom, with the emission of secondary particles (photoelectron, Auger electrons or/and fluorescence x-rays).
Coherent scattering (Rayleigh): the photon is just deflected without loosing energy (elastic scattering).
Incoherent scattering (Compton, Raman): The photon interacts with an atomic electron exchanging energy and momentum.
Pair production: the creation of an electron-positron pair by the photon in a nuclear field. This process can only occur if the photon energy is greater than 2mc2 (the rest energy of the two created particles, ~1.022 MeV), therefore it is not accessible for "typical" x-rays.
The DABAX files CrossSec_<name>.dat contain tabulations of one, several or all of the interactions channels. They can be visualized and compared using the xcrosssec application, which can also be used for the computation of the attenuation coefficient.
The attenuation coefficient ml (dimension L-1), is relatic to the the atomic attenuation coefficient or interaction cross section (dimensions L-2) as:
![]()
(n is number of scatters per unit of volume)
Another non-DABAX application for cross sections is XXCOM, which uses the widely used XCOM program.
Attenuations (often also called filters) are material plates inserted in the beam with the aim of reducing its intensity. As attenuation coefficient is energy-dependent, the attenuation effect is energy-dependent, thus it modifies the spectral distribution of the x-ray beam.
Attenuation coefficients can be calculated from tabulated cross sections using the xcrosssec and xxcom programs. Although xf1f2 also calculates the (photoelectric) attenuation coefficient, is not recommended to use it for attenuation calculations as it ignores inelastic scattering which may be crucial for high photon energies and low atomic number elements.
The intensity I of an x-ray beam after been travelled in a material of plate of thickness t is given by the well-known exponential law:
![]()
where I0 is the incoming intensity. The application xpower uses this formula to calculate the effect of up to five optical elements (attenuators and mirrors) placed in an x-ray beam. Their effect is computes as a function of the x-ray energy.
The reflectivity of a thick reflecting surface (mirror) is computed using the Fresnel formulas. They require to know the refractive index, which is obtained from DABAX data files. Again, reflectivity is energy dependent, because of the dependence of the refractive index on photon-energy. Two applications can be used:
xf1f2: Calculates the reflectivity of mirrors versus photon-energy, incidence angle or both.
xpower. Calculates the reflectivity of mirrors versus photon energy. It may apply this reflectivity to a source spectrum and combine it with attenuators and a monochromator.
Crystals are used for x-ray monochromators. Almost all x-ray monochromators in synchrotron beamlines use perfect crystals like silicon or germanium. For describing the crystal diffraction by perfect crystals, the dynamical theory of diffraction should be used. Several calculation algorithms are implemented in XOP crystal application to deal with different kind of crystals:
Flat perfect crystals diffraction profiles, like Si, Ge or diamond can be calculated using the xcrystal code. It can calculate angular scans for a given photon energy, or energy scans for a given incident angle. Any crystal structure may be used (definition parameters are in DABAX files CrystalStructure.dat and CrystalCell.dat). It includes a simple model for the temperature factor.
An alternative non-DABAX program for flat crystal diffraction profiles is xinpro. However, we recommend the use of xcrystal
Mosaic crystal reflectivity can be computed using xcrystal
The diffraction profiles of curved crystals is in general different from the flat ones. Several models are available in the xcrystal_bent program:
Multilamelar model, useful for computing diffraction profiles of curved crystal in Bragg geometry
Penning-Polder model, for crystals in Laue geometry.
Takagi-Taupin. This model is in experimental status so results should be taken with extreme prudence. It is recommended not to use it if the user is not familiar with the theory
A program for displaying multiple reflections and calculate unweganregun patterns and glitches plots is MARE. It uses a simplified model (no dynamical theory) for line intensities.
The program XPOWDER simulates diffraction pattern of powder samples.
We included in XOP a basic program for multilayer calculations: mlayer. It can calculate the multilayer (periodic and graded) reflectivity versus photon energy (for a constant incidence angle) or versus incidence angle (for constant energy). This program is limited because it can only deal with elements (not compounds) and it does not take into account the effect of the roughness at the interfaces. Users interested in more sophisticated multilayer modeling and fit with experimental data can use the IMD code, available as an XOP extension.
A program for calculating the focusing effect of Compound refractive lenses using a simplified ray-tracing models is also available: crl