Fourier Interpolation of the dynamical matrix¶
This script calculates Fourier Transform of the dynamical matrix.
The usage is
make_TDS_Fourier castep_filename input_filename
the file castep_filename can be either the name of the original castep output or the associated hdf5 file. In any case the associated hdf5 file must exist already: make_TDS_Simmetrization must have been run beforehand in order to fill by symmetry operations the missing part of the Brillouin zone. The Fourier transform is performed by summing over the whole Brillouin zone the periodic dynamical matrix
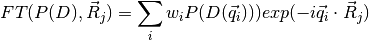
where
 runs over all provided q-points (the original and the simmetry-replicated ones). The vectors
runs over all provided q-points (the original and the simmetry-replicated ones). The vectors
 are defined in real space on the Bravais lattice of the crystal.
are defined in real space on the Bravais lattice of the crystal.The Dynamical matrix is defined in periodic notation in
 space. It is obtained on the basis of eigenvectors
space. It is obtained on the basis of eigenvectors  and eigenvalues
and eigenvalues  :
: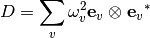
provided by the input file. If the eigenvectors are periodic in
 the matrix is already periodic, but often, as it is the case
for castep, the natural choice is outputting Bloch-Theorem satisfying vectors. In this latter case the periodicity of the dynamical matrix
is ensured by adding/removing the proper phases.
the matrix is already periodic, but often, as it is the case
for castep, the natural choice is outputting Bloch-Theorem satisfying vectors. In this latter case the periodicity of the dynamical matrix
is ensured by adding/removing the proper phases.The input_file must set the variables:
- Nfour_interp
- this variable is very important. The cubic grid counts
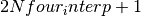 points along each primitive Bravais axis.
This number must be large enough to exceed the spatial range of the forces in order to cope with the variation of the Dynamical matrix: the longer the interaction distance, the higher
the necessary Nfour_interp will be. A too large Nfour_interp may however cause artefacts. In this case either you
have to lower it, or if it is really necessary to keep long distance interactions you have to increase the number of
calculated q-points in the input file.
points along each primitive Bravais axis.
This number must be large enough to exceed the spatial range of the forces in order to cope with the variation of the Dynamical matrix: the longer the interaction distance, the higher
the necessary Nfour_interp will be. A too large Nfour_interp may however cause artefacts. In this case either you
have to lower it, or if it is really necessary to keep long distance interactions you have to increase the number of
calculated q-points in the input file.
- APPLYTIMEREVERSAL
using a python syntax
The input variables are documented with docstrings below
-
make_TDS_Fourier.APPLYTIMEREVERSAL= 1 this is one by default. Must be coherent with previous steps
-
make_TDS_Fourier.Nfour_interp= 5 The number of points in each direction of the 3D reciprocal grid